1371. Quick answers
Joe is fond of computer games. Now, he must
solve a puzzling situation. In front of his eyes lies a huge map with fortified
towns. His enemy is a very powerful and tricky character who can connect and
disconnect the towns by giving some commands. Two towns are connected if they
have been directly connected or interconnected through some other connected
towns at some moment in time. When a town is disconnected it gets isolated and
clears its own connection history, not the connection history of the other towns.
Each connection is bidirectional. Initially the towns are isolated. Joe is
asked to answer quickly if two towns are connected, according to the history of
the character’ commands.
Write a program which based on input
information, counts the number of yes answers and the number of no
answers to questions of the kind: is towni connected with townj?
Input. Each data set stands for a particular map and the
associated character's commands, as follows:
1) The number of towns on the map n (n
≤ 10000);
2) A list of commands of the form:
a) c towni townj,
where towni and townj
are integers from 1 to no_of_towns. The command means that towni and townj
get connected.
b) d towni, where towni is an integer from 1 to no_of_towns. The command means that towni gets disconnected.
c) q towni townj, where towni and townj are integers from 1 to no_of_towns. The command stands for the question: is towni connected with townj?
d) e, that ends the list of
commands Each command is on a separate line.
Commands (a), (b), (c) can appear in any
order. The towns’ connectivity is updated after each command of type (a) or (b).
Each command of type (c) is processed according to the current configuration.
Output. The program
prints these two numbers on the same line, in the order: n1, n2
as shown in sample output.
Example. For
example, the input illustrated bellow corresponds to only one data set which
stands for a map with 4 fortified towns. The character gives 9 commands. There
are n1 yes answered questions and n2
no answered questions.
|
Sample
input |
Sample
output |
|
4 c 1 2 c 3 4 q 1 3 c 2 3 q 1 4 d 2 q 4 1 q 2 4 e |
2 , 2 |
SOLUTION
data structures - dsu
Algorithm analysis
Let’s introduce the concept of a city identification code.
Initially, we put Id[i] = i. When processing queries of type c
and q on a system of disjoint sets, we will process array cells that
correspond to the identification codes of cities. Let MaxID contain the minimum
still unused city code (initially there are n cities, let MaxID = n
+ 1). Then we’ll disconnect
the city (a query of the d towni type) by
assigning a new id code to the towni
(for example, Id[i] = MaxID ++). Thus, the old connections (the memory
of the cities) remain, and the new city actually becomes disconnected from the
rest.
For example, to unite cities i and j, the function Union(Id[i], Id[j]) will be called.
The representative of the city i is returned by the function Repr(Id[i]).
Example
Initialize the array mas
and the identification codes array. The identification code of each city initially
equals to the number of the city itself (Id[i] = i).
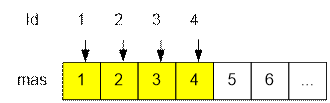
Process the first three queries. In two queries, cities 1 and 2, 3 and 4 are connected. The graph has the form:

The
answer to the query q(1,
3) is no,
since the vertices 1 and 3 are not connected.
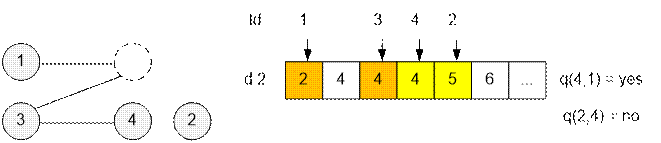
The next query unites cities 2 and 3. Vertices 1 and
4 become connected. Query q(1, 4) returns yes.

The next query (d
2) disconnects city 2. City 2 is assigned a new id code. The minimum unused
city code is 5. Set Id[2] = 5. Cities 4 and 1 are connected (the connection is not broken). Cities 2 and 4 are not connected
with each other. For example, for a query q(2, 4) we
must check if Repr (Id[2]) and Repr (Id[4]) (or Repr(5) and
Repr(4)) are equal. Taking into account that Repr(5) = 5, Repr(4) = 4, we
conclude that vertices 2 and 4 are disconnected.
Algorithm realization
Let’s declare an
array mas used by the disjoint set dat structure. Declare array Id that contains the current
city identification codes.
#define MAX 100010
int mas[MAX], Id[MAX];
Function Repr finds
a representative of the set that contains vertex n.
int Repr(int
n)
{
if (n ==
mas[n]) return n;
return mas[n]
= Repr(mas[n]);
}
Function Union unites
sets that contain vertices x and y.
int Union(int
x,int y)
{
int x1 =
Repr(x),y1 = Repr(y);
mas[x1] = y1;
return (x1 !=
y1);
}
The main part of the program.
while(scanf("%d\n",&n)
== 1)
{
Initialization of arrays and
variables.
for(i = 1; i
< MAX; i++) mas[i] = i, Id[i] = i;
MaxID = n + 1;
n1 = n2 = 0;
Process sequentially
the queries.
while(scanf("%c",&c), c != 'e')
{
Unite the cities towni and townj.
if (c == 'c')
{
scanf("%d
%d\n",&i,&j);
Union(Id[i],Id[j]);
}
Disconnect the city towni.
if (c == 'd')
{
scanf("%d\n",&i);
Id[i] = MaxID++;
}
Check if the cities towni and townj are connected.
if (c == 'q')
{
scanf("%d
%d\n",&i,&j);
if
(Repr(Id[i]) == Repr(Id[j])) n1++; else n2++;
}
}
Print the answer.
printf("%d ,
%d\n",n1,n2);
}